概率

概率,或然率（Probability）
　　或然率即或然比，也叫概率和機會率：是對可能性在量上的一種科學說明和測定。它是要測定的偶然事件的數目與全部可能發生的偶然事件的總數之間的比率。如果n是可能發生的偶然事件的總數，而m是要測定的偶然事件的數目，那么，或然率就是m／n。m和n的比值在零和一之間，如果或然率等於零，就說明沒有可能或不可能；如果或然率等於一，就說明有百分之百的可能，這時的可能就完全成了必然。測定或然率是人們實踐的需要，目前在自然科學和社會科學中得到廣泛的應用。

　　或然率有下列兩種理論：

　　一、理論或然率（Theoretical Probability）：即根據事件本性推理而得的或然率，又稱先天（Priori）或然率。例如：一枚硬幣有正反兩面，將其拋擲，其正面朝上之或然率，不待試驗即可推知其爲二分之一；又例如：若一摸彩箱中共有彩券三十張，其中有獎之彩券共十張，則可推知其中獎之或然率爲三分之一。

　　二、經驗或然率（Empirical Probability）：即根據實際現象歸納衆多次數而得之或然率。例如：將一枚硬幣拋擲一百次，若其出現正面朝上之次數爲五十二次，即稱拋擲該枚硬幣出現正面朝上之或然率爲52/100=0.52；又例如：若甲縣某年內共出生嬰兒四千八百六十五人，其中男嬰爲二千五百三十四人，則該縣男嬰出生之或然率即爲2534/4865=0.52。此種或然率又稱後天的（Posteriori）或然率。

　　或然率具有三個基本公理：

　　公理1：P{A}≥0 P{A}代表事件A發生的或然率，這個公理表示一個事件發生的或然率必須大於0或等於0。如果一個事件A可能發生，那么它的或然率P{A}必然大於0，假使事件A不可能出現，則它發生的或然率等幹0。換句話說，任何一事件發生的或然率不可能是負值。

　　公理2：P{S}=1，S代表所有可能發生的全部事件，P{S}代表它們發生的或然率。這個公理表示在所有可能發生的各個事件中，必然有一個事件發生的或然率等於1。例如一個硬幣只有正，反兩面，投擲的結果不是正面就是反面，所有可能發生的事件共有二個，一個是出現正面，一個是出現反面。用S代表所有可能發生的事件的全體，那么用A表示正面，用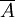表示反面，這樣S與A、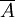三者的關系可以表示爲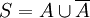(U這個符號讀作“並”，意思指“或者”即A或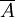至少有一個發生。在這裏的作用與加法符號相同)。這樣投擲一枚硬幣出現正面與反面的或然率就可以寫作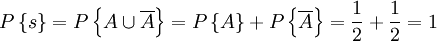

　　假設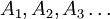這樣一些事件不能並存，互相排斥，就可以用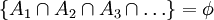表示事件同時發生不存在，也就是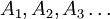等事件同時出現是不可能的。(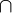這個符號讀作“交”表示“乘積”指A₁和A₂和A₃等事件同時發生)。由此可得：

　　公理3:b2b6.png">

　　公理3表示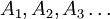這些事件中任一事件都不能與其它事件同時並存，則A₁、A₂、A₃事件發生的或然率等於各個事件發生或然率之和。

　　例如；在一個袋中有各色的小球10個，僅知道其中有紅球A₁一個，白球A₂二個，蘭球A₃三個，這三個事件是互相排斥，也就是說是白球就不可能是紅球，是紅球就不可能是蘭球。如果從袋中抽取一個球，問這個球是紅、白、蘭三色中任何一色時的或然率爲多少?根據公理3得

 
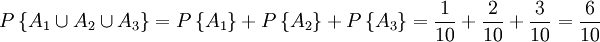
　　隨着人們遇到問題的復雜程度的增加，等可能性逐漸暴露出它的弱點，特別是對於同一事件，可以從不同的等可能性角度算出不同的概率，從而產生了種種悖論。另一方面，隨着經驗的積累，人們逐漸認識到，在做大量重復試驗時，隨着試驗次數的增加，一個事件出現的頻率，總在一個固定數的附近擺動，顯示一定的穩定性。R.von米澤斯把這個固定數定義爲該事件的概率，這就是概率的頻率定義。從理論上講，概率的頻率定義是不夠嚴謹的。A.H.柯爾莫哥洛夫於1933年給出了概率的公理化定義。
概率的嚴格定義
　　設E是隨機試驗，S是它的樣本空間。對於E的每一事件A賦於一個實數，記爲P(A)，稱爲事件A的概率。這裏P(·)是一個集合函數，P(·)要滿足下列條件：
（1）非負性：對於每一個事件A，有P(A)≥0;
（2）規範性：對於必然事件S，有P(S)=1;
（3）可列可加性：設A1，A2……是兩兩互不相容的事件，即對於i≠j，Ai∩Aj=φ，（i,j=1,2……），則有P（A1∪A2∪……）=P（A1）+P（A2）+……

 
　　如果一個試驗滿足兩條：
（1）試驗只有有限個基本結果
（2）試驗的每個基本結果出現的可能性是一樣的。
這樣的試驗，成爲古典試驗。
對於古典試驗中的事件A，它的概率定義爲：
P(A)=m/n，n表示該試驗中所有可能出現的基本結果的總數目。m表示事件A包含的試驗基本結果數。這種定義概率的方法稱爲概率的古典定義。

 
　　在一定條件下，重復做n次試驗，nA爲n次試驗中事件A發生的次數，如果隨着n逐漸增大，頻率nA/n逐漸穩定在某一數值p附近，則數值p稱爲事件A在該條件下發生的概率，記做P(A)=p。這個定義成爲概率的統計定義。
在歷史上，第一個對“當試驗次數n逐漸增大，頻率nA穩定在其概率p上”這一論斷給以嚴格的意義和數學證明的是早期概率論史上最重要的學者雅各布·伯努利（Jacob Bernoulli，公元1654年～1705年）。
從概率的統計定義可以看到，數值p就是在該條件下刻畫事件A發生可能性大小的一個數量指標。
由於頻率nA/n總是介於0和1之間，從概率的統計定義可知，對任意事件A，皆有0≤P(A)≤1，P(Ω)=1，P(Φ)=0。
Ω、Φ分別表示必然事件（在一定條件下必然發生的事件）和不可能事件（在一定條件下必然不發生的事件）。

 
古典概率相關
　　古典概率討論的對象局限於隨機試驗所有可能結果爲有限個等可能的情形，即基本空間由有限個元素或基本事件組成，其個數記爲n，每個基本事件發生的可能性是相同的。若事件A包含m個基本事件，則定義事件A發生的概率爲p（A）=m/n，也就是事件A發生的概率等於事件A所包含的基本事件個數除以基本空間的基本事件的總個數，這是P.-S.拉普拉斯的古典概率定義，或稱之爲概率的古典定義。歷史上古典概率是由研究諸如擲骰子一類賭博遊戲中的問題引起的。計算古典概率，可以用窮舉法列出所有基本事件，再數清一個事件所含的基本事件個數相除，即借助組合計算可以簡化計算過程。
幾何概率相關
　　幾何概率若隨機試驗中的基本事件有無窮多個，且每個基本事件發生是等可能的，這時就不能使用古典概率，於是產生了幾何概率。幾何概率的基本思想是把事件與幾何區域對應，利用幾何區域的度量來計算事件發生的概率，布豐投針問題是應用幾何概率的一個典型例子。
在概率論發展的早期，人們就注意到古典概率僅考慮試驗結果只有有限個的情況是不夠的，還必須考慮試驗結果是無限個的情況。爲此可把無限個試驗結果用歐式空間的某一區域S表示，其試驗結果具有所謂“均勻分布”的性質，關於“均勻分布”的精確定義類似於古典概率中“等可能”只一概念。假設區域S以及其中任何可能出現的小區域A都是可以度量的，其度量的大小分別用μ(S)和μ(A)表示。如一維空間的長度，二維空間的面積，三維空間的體積等。並且假定這種度量具有如長度一樣的各種性質，如度量的非負性、可加性等。
◆幾何概率的嚴格定義
設某一事件A（也是S中的某一區域），S包含A，它的量度大小爲μ(A)，若以P(A)表示事件A發生的概率，考慮到“均勻分布”性，事件A發生的概率取爲：P(A)=μ(A)/μ(S)，這樣計算的概率稱爲幾何概率。
◆若Φ是不可能事件，即Φ爲Ω中的空的區域，其量度大小爲0，故其概率P(Φ)=0。
獨立試驗序列
　　假如一串試驗具備下列三條：
（1）每一次試驗只有兩個結果，一個記爲“成功”，一個記爲“失敗”，P{成功}=p，P{失敗}=1-p=q
（2）成功的概率p在每次試驗中保持不變
（3）試驗與試驗之間是相互獨立的。
則這一串試驗稱爲獨立試驗序列，也稱爲bernoulli概型。
必然事件與不可能事件
　　在一個特定的隨機試驗中，稱每一可能出現的結果爲一個基本事件，全體基本事件的集合稱爲基本空間。隨機事件（簡稱事件）是由某些基本事件組成的，例如，在連續擲兩次骰子的隨機試驗中，用Z，Y分別表示第一次和第二次出現的點數，Z和Y可以取值1、2、3、4、5、6，每一點（Z，Y）表示一個基本事件，因而基本空間包含36個元素。“點數之和爲2”是一事件，它是由一個基本事件（1，1）組成，可用集合{（1，1）}表示“點數之和爲4”也是一事件，它由（1，3），（2，2），（3，1)3個基本事件組成，可用集合{（1，3），(3，1)，（2，2)}表示。如果把“點數之和爲1”也看成事件，則它是一個不包含任何基本事件的事件，稱爲不可能事件。在試驗中此事件不可能發生。如果把“點數之和小於40”看成一事件，它包含所有基本事件，在試驗中此事件一定發生，所以稱爲必然事件。若A是一事件，則“事件A不發生”也是一個事件，稱爲事件A的對立事件。實際生活中需要對各種各樣的事件及其相互關系、基本空間中元素所組成的各種子集及其相互關系等進行研究。
【隨機事件，基本事件，等可能事件，互斥事件，對立事件】
在一定的條件下可能發生也可能不發生的事件，叫做隨機事件。
一次實驗連同其中可能出現的每一個結果稱爲一個基本事件。
通常一次實驗中的某一事件由基本事件組成。如果一次實驗中可能出現的結果有n個，即此實驗由n個基本事件組成，而且所有結果出現的可能性都相等，那么這種事件就叫做等可能事件。
不可能同時發生的兩個事件叫做互斥事件。
必有一個發生的互斥事件叫做對立事件。
即P（必然事件）=1
P（可能事件）=(0-1)（可以用分數）
P（不可能事件）=0
性質
　　性質1．P(Φ)=0.
性質2（有限可加性）．當n個事件A1，…，An兩兩互不相容時：　P(A1∪。。.∪An)=P(A1)+...+P(An)．
性質3．對於任意一個事件A：P(A)=1-P(非A)．
性質4．當事件A,B滿足A包含於B時：P(B-A)=P(B)-P(A)，P(A)≤P(B)．
性質5．對於任意一個事件A，P(A)≤1．
性質6．對任意兩個事件A和B，P(B-A)=P(B)-P(AB)．
性質7（加法公式）．對任意兩個事件A和B，P(A∪B)=P(A)+P(B)-P(A∩B)．
（注：A後的數字1，2，．．．，n都表示下標．）
頻率與概率
　　對事件發生可能性大小的量化引入“概率”．
“統計規律性”
獨立重復試驗總次數n,事件A發生的頻數μ，
事件A發生的頻率Fn(A)=μ/n,A的頻率Fn(A)有沒有穩定值？
如前人做過的擲硬幣的試驗(P.44下面表)
如果有就稱頻率μn的穩定值p爲事件A發生的概率記作P(A)=p[概率的統計定義]
P(A)是客觀的，而Fn(A)是依賴經驗的。
統計中有時也用n很大的時候的Fn(A)值當概率的近似值。

 
　　1．[非負性]：任何事件A，P(A)≥0
2．[完備性]：P(Ω)=1
3．[加法法則]如事件A與B不相容，即如果AB=φ，則P(A+B)=P(A)+P(B)
加法法則
　　如事件A與B不相容，A+B發生的時候，A與B兩者之中必定而且只能發生其中之一。獨立重復地做n次實驗，如記事件A發生的頻數爲μA、頻率爲Fn(A) ，記事件B發生的頻數爲μB 、頻率爲Fn(B) ，事件A+B發生的頻數爲μA+B 、頻率爲Fn(A+B) ，易知：μA+B =μA +μB，∴Fn(A+B) = Fn(A) + Fn(B) ,它們的穩定值也應有：P(A+B)=P(A)+P(B)[加法法則]如事件A與B不相容，即如果AB=φ，則 P(A+B)=P(A)+P(B)即：兩個互斥事件的和的概率等於它們的概率之和。請想一下：如A與B不是不相容，即相容的時候呢？進一步的研究得： P(A+B)=P(A)+P(B)-P(AB)這被人稱爲：“多退少補”！
模糊和概率
　　1.是否不確定性就是隨機性？似然比、概率是否代表了所有的不確定性？
Bayesian camp：概率是一種主觀的先驗知識，不是一種頻率和客觀測量值
Lindley：概率是對不確定性唯一有效並充分的描述，所有其他方法都是不充分的
相似：通過單位間隔[0,1]間的數來表述不確定性，都兼有集合、相關、聯系、分布方面的命題
區別：對待。經典集合論，

代表概率上不可能的事件。而模糊建立在
（1）是否總是成立的？
考慮能否邏輯上或部分地違背“無矛盾定理”（Aristotle的三個‘思考定理’之一，同時排中定理同一
性定理這些都是非黑即白的經典定理。）模糊（矛盾）的產生，就是西方邏輯的結束
（2）是否可以推導條件概率算子？
經典集合論中：
模糊理論：考慮超集是其子集的子集性程
度，這是模糊集合的特有問題。
2.模糊和概率：是否與多少
模糊是事件發生的程度。隨機是事件是否發生的不確定性。
例子：明天有20%的幾率下小雨（包含復合的不確定性）
停車位問題
一個蘋果在冰箱裏的概率和半個蘋果在冰箱裏
事件倒轉，地球演變恢復原點
模糊是一種確定的不定性（deterministic uncertainty），是物理現象的特性。用模糊代表不確定性的
結果將是震撼的，人們需要重新審視現實模型。